コロナの感染者数、なぜ対数グラフ⁉指数関数ってなんだっけ⁉

新型コロナウイルスの感染がなかなか終息しません。

最近見かけるようになったのが、
「対数グラフ」「指数関数的増加」という言葉を耳にするようになりました。

高校の時に習ったような・・・とかすかな記憶を頼りに見られている方もおられるのではないでしょうか。

指数関数的に増加する感染者数

指数関数的にという言葉。

理系の大学を出られてエンジニアで働かれている人であれば使う方もいますが、
普段の生活では全くきかない言葉ですね。

指数関数的増加とは、簡単にいうと倍々で増えていくということです。

1週間毎に倍に増えていくというとある病気があるとします。

1週間毎に、2倍、2倍と増えていきますので、
1週目は1人、2週目は2人、3週目は4人と増加するということを仮定します。

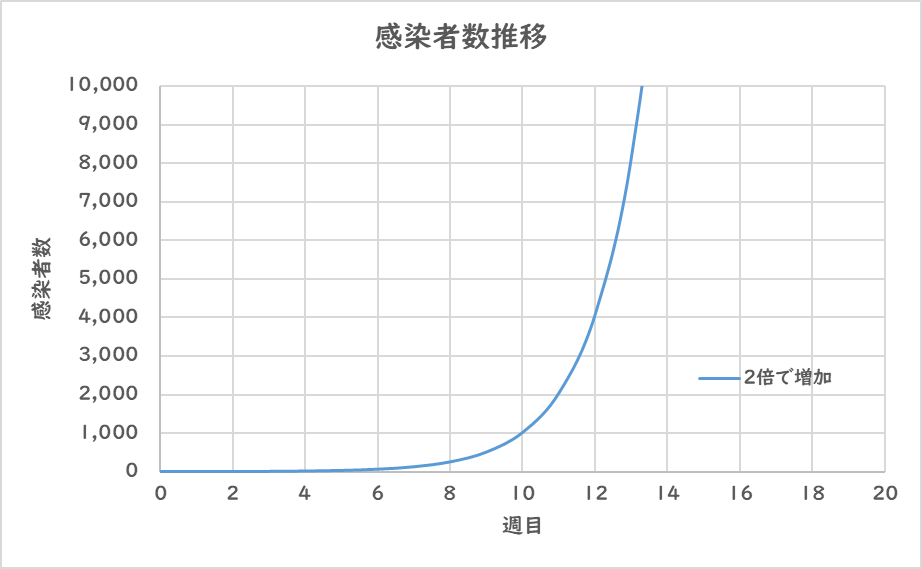
この場合感染者数の推移のグラフはこのようになります。

このグラフが典型的な指数関数的に増加を示すグラフです。

感染者数を対数グラフで見る意味についてみていきます。

先ほどのグラフは、1週間毎に感染者が倍になっていくグラフでした。

さらにここに1週間毎に3倍になる街があったとし、
この推移を同様にグラフに示すとこのようになります。

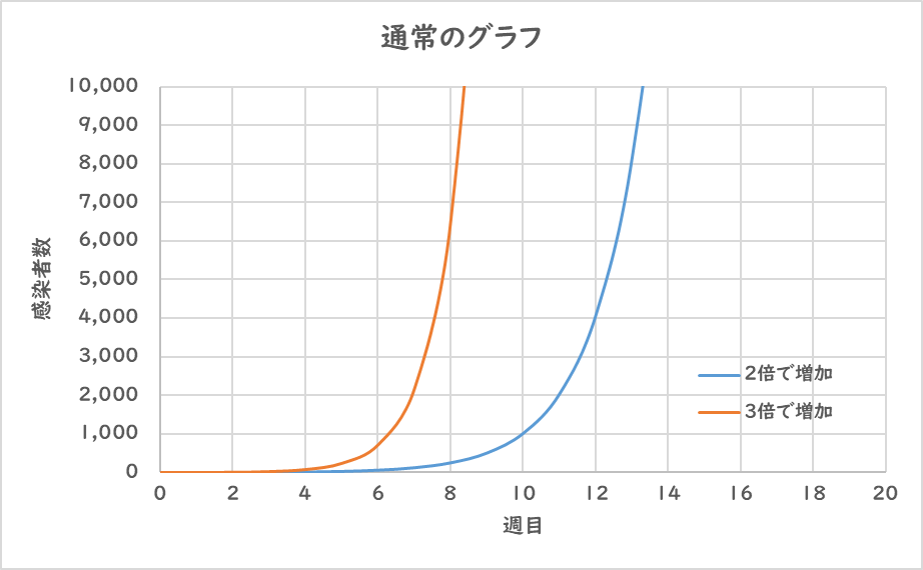
当然ですがオレンジ線の3倍増加は2倍増加と比較して圧倒的に感染者数が増加することがわかります。

ここで重要なポイントがもう一つ。

4週目までの絶対数が少ないときの違いがほとんど違いが判りません。

これでは初期のときの判断が難しくその後の対応が変わってきます。

ここで出てくるのが対数グラフです。

縦軸のメモリが、10のべき乗で表されているグラフです。

このグラフは縦軸だけが対数なので、正式には片対数グラフといいます。

ここで先ほど2倍増加と、3倍増加の感染者数の推移を対数グラフで表すと
このようになります。

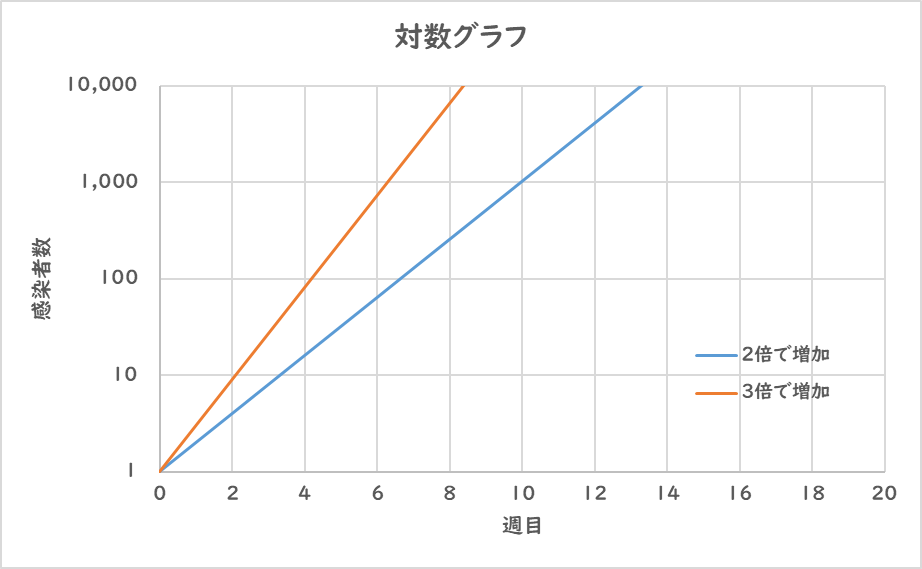
通常のグラフでは見えてこなかった2週目、4週目のような絶対数がまだ少ないときでも差もはっきり見えることができます。

また対数グラフで指数関数的に増加するものを、直線で表すことができるので、
この増加率の違いをいち早く気づくことができ、将来の推移の見立てが可能となります。

増加率の変化もこのグラフの傾きで見ることができます。

新型コロナウイルス感染者数を示したグラフがコチラです。

感染者数を増えているのはわかりますが、
その増加率が上昇しているのか鈍化しているかがわかりにくいです。

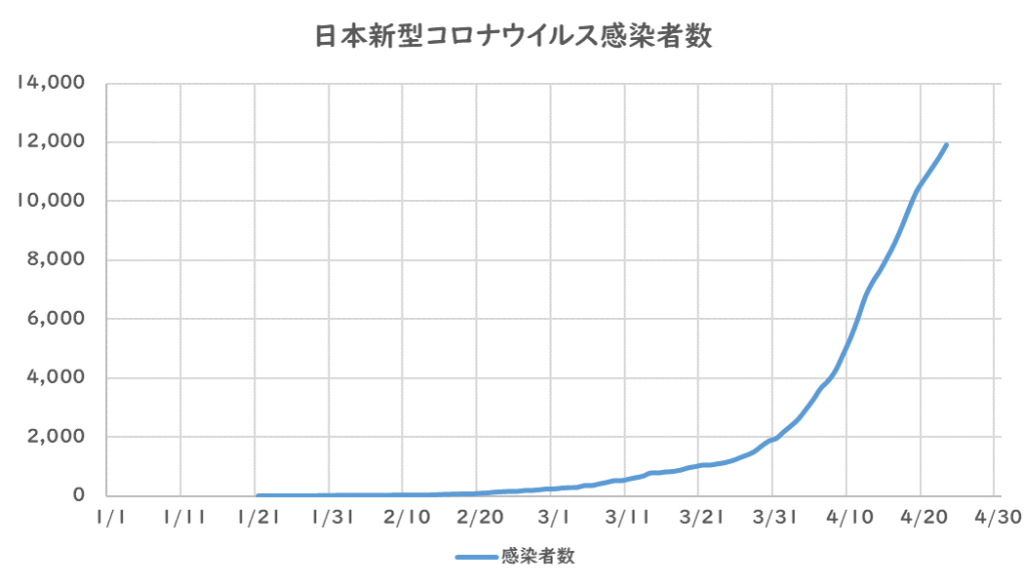
そこで対数グラフの出番です。

対数グラフでこの感染者数を表すとこのようになります。

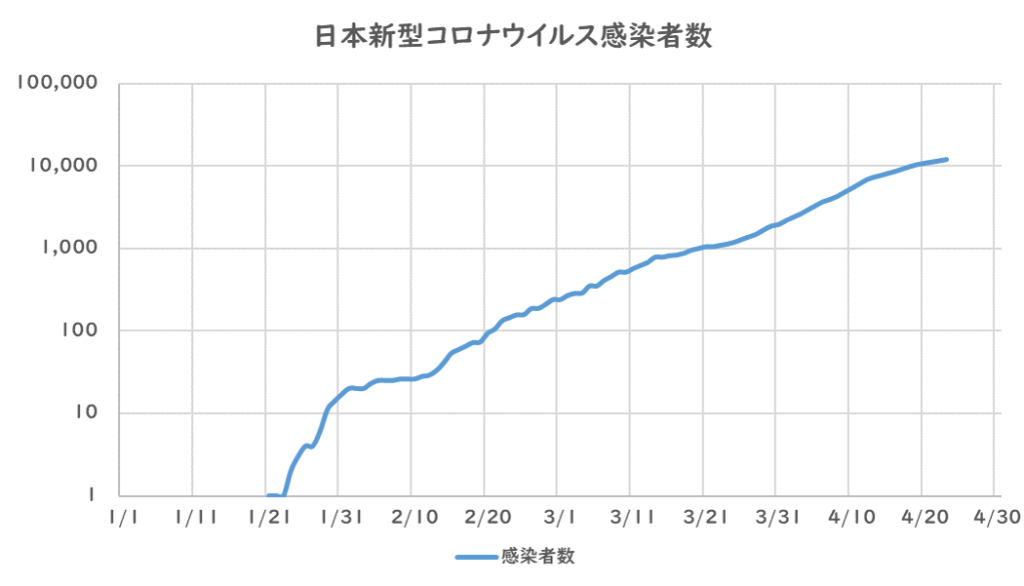
3月下旬から4月上旬まで、傾きが急で、増加率が高かったですが、
4月中旬ごろには鈍化傾向がうっすら見えてきたのがわかります。

また3月21日頃に一旦鈍化しかかったのもわかりますが、その後傾きが急になっているのもわかります。

報道等でもあった通り、3月の3連休による影響があったものとみられます。

最後までお読みいただきありがとうございました。